Mathematics, a discipline that has existed for millennia, has played a pivotal role throughout history in explaining the world around us. However, it can also be a source of confusion when we encounter unfamiliar operations.
In today’s article, we’ll embark on a journey to compare two fractions and determine which one is bigger. Is 1/2 bigger than 2/3?
Fractions, one of the most fundamental mathematical concepts, serve as tools to represent parts of a whole. To effectively compare them, it’s helpful to visualize them as slices of a pizza or a pie.
Imagine a pizza divided into equal portions.
- If we have 1/2 of the pizza, it means we have one of the two slices.
- If we have 2/3 of the pizza, it means we have two out of the three slices into which the pizza has been divided.
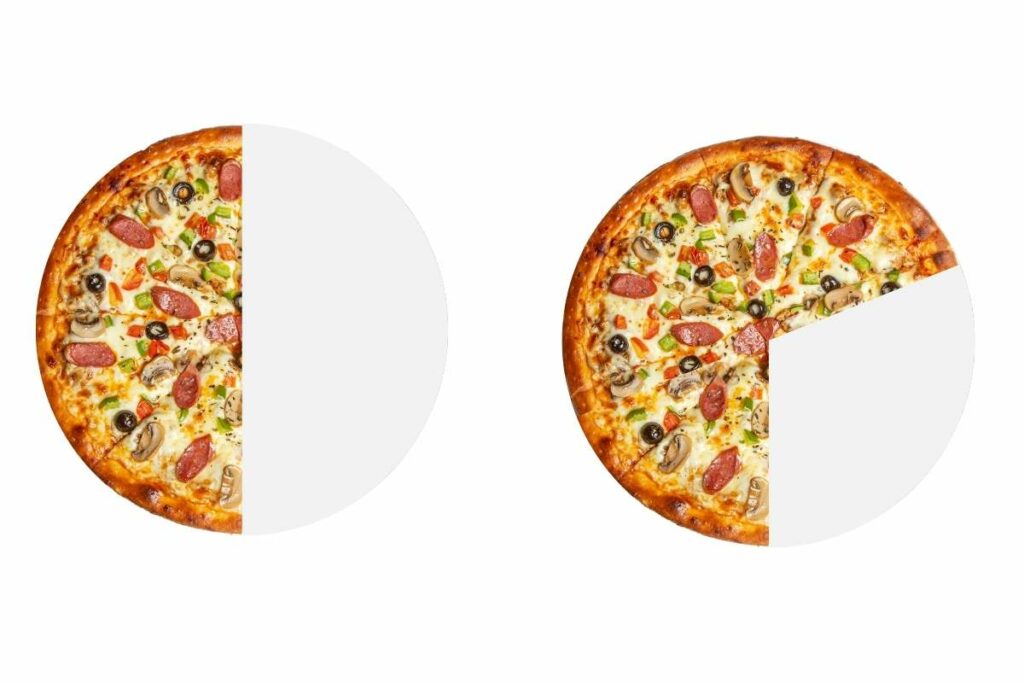
At first glance, 2/3 of the pizza appears larger than 1/2.
While we’ll delve into more details later, to answer your question upfront:
Is 1/2 bigger than 2/3?
No, 1/2 is smaller than 2/3. 1/2 represents 0.5, while 2/3 represents 0.66.
To confirm this mathematically, we can employ two methods:
Method 1: Converting Fractions to a Common Denominator to determine if 1/2 is bigger than 2/3
The least common multiple (LCM) of 2 and 3 is 6.
We convert 1/2 to 3/6 by multiplying both the numerator and denominator by 3:
- 1/2 = 3/6
And we convert 2/3 to 4/6 by multiplying both numerator and denominator by 2:
- 2/3 = 4/6
Now, we can easily compare both fractions since they have a common denominator:
- 3/6 represents three slices of a pie divided into six parts.
- 4/6 represents four slices of the same pie divided into six parts.
Clearly, 4/6 is larger than 3/6, and consequently, 1/2 is smaller than 2/3.
2. Method 2: Representing Fractions on a Number Line
To represent fractions on a number line, follow these steps:
- Locate the 0 (zero) at one end of the line and mark equal intervals based on the denominator.
- Divide the first line into two equal parts since the denominator is 2.
- Divide the second line into three parts since the denominator is 3.
- On the first line:
- Mark 1/2 at the first point to the right of 0.
- On the second line:
- Mark 1/3 at the first point to the right of 0.
- Mark 2/3 at the second point to the right of 0.
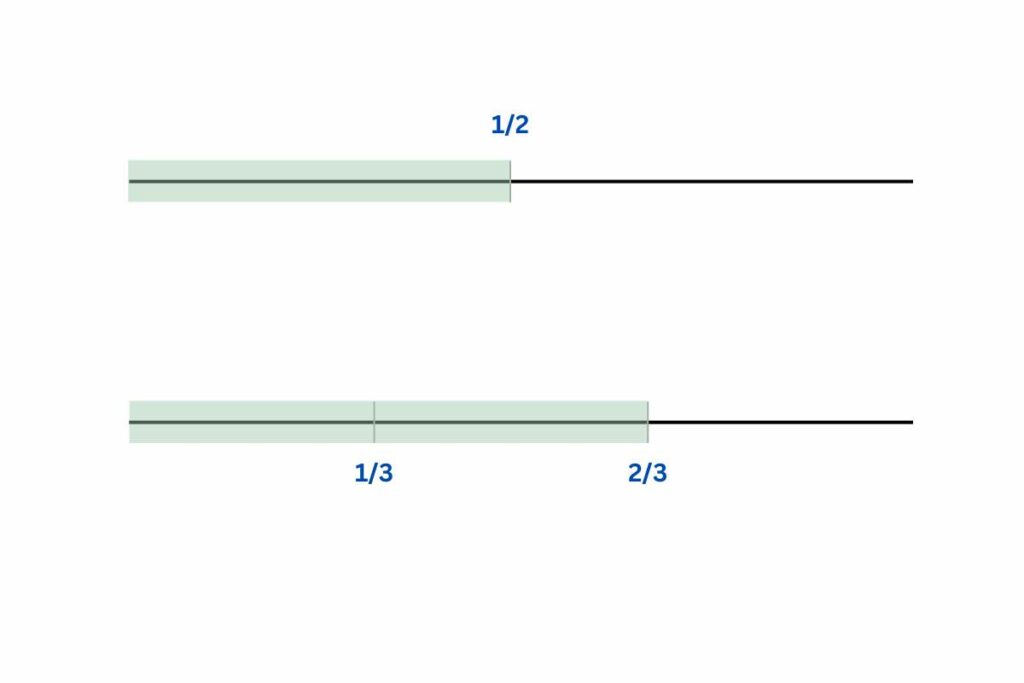
Observing the lines, we can clearly see that 2/3 lies further to the right than 1/2, confirming that 1/2 is not larger than 2/3.
Conclusion: Unveiling the Winner. Is 1/2 bigger than 2/3?
Both the pizza slice visualization and the conversion to a common denominator or representation on a number line help us grasp and compare the value of fractions, revealing that 2/3 is indeed larger than 1/2. Therefore, 1/2 is not bigger than 3/4.